【土地家屋調査士試験】
平成元年（1989年）度「E点」

E点の座標値を求める方法は3種類あります。次の3つです。

1. 方向角×斜辺
2. 内分点の公式（or 比の計算）
3. 直線の方程式

土地家屋調査士試験の座標値の計算問題は、この3つの方法で解くものが多いです。ここではまずは一番上の「方向角×斜辺」の説明をしていきます。

ここからは平成元年（1989年）度の試験問題（点Eの座標値を求める）を題材にして「方向角×斜辺」の説明をしていきたいと思います。

数学座標のときは

• sinθ×斜辺＝高さ（＝Y座標）
• cosθ×斜辺＝底辺（＝X座標）

という公式が使えました。

高校の教科書風にいうと

• sinθ＝高さ/斜辺
• cosθ＝底辺/斜辺

でしたね。

しかし、土地家屋調査士試験は問題用紙に掲載されている測量成果が測量座標を元にして作られているため、「高さ＝Y座標 底辺＝X座標」ではなくなっています。①. 数学座標は縦軸（↑）がYで、横軸（→）がXでしたが、測量座標は縦軸（↑）がXで、横軸（→）がYです。②. そのため測量座標は「高さ＝X座標 底辺＝Y座標」になります（一見、XとYが入れ替わっているように見える。しかし、実は入れ替わっているのはXとYではなく高さと底辺です。詳しくは後述します。とりあえず今は以下の画像を参照し、上記①.と②.の2つのことを確認のこと）。

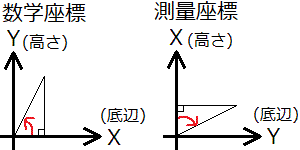
また、数学座標のときは角度の進む向きは「反時計回り」（左回り（↖））でしたが、測量座標の場合は「時計回り」（右回り（↘））に進みます。この角度の進む向きは、数学座標を測量座標に変更するにあたって、人為的に何か手を加えて、あらためて角度を逆向きにしたものではありません。数学座標も測量座標も、角度はどちらもX軸から出発していますし、数学座標の画像に一切手を加えなくても、数学座標の画像を上下反転させて左回転、あるいは左右反転して右回転すれば測量座量は作れます。

私が何を言っているかが分からない方は、裏側が透けて見えるような薄い紙の右下（↘）に小さく濃く数学座標の絵を書いて、その紙を下から内側に斜めに（↖の向きに）大きく折り曲げてみてください。表面の数学座標は、裏面から見れば測量座標になります（これは上下反転させて左回転のケースです。もし左上（↖）に書いた数学座標を上から内側に斜めに（↘の向きに）折り曲げると、左右反転して右回転のケースになります）。

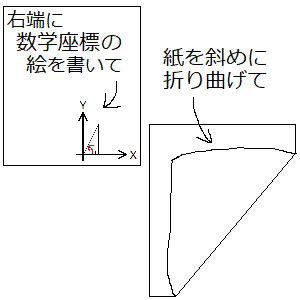
数学座標も測量座標も同じものです。ただ座標全体の向きや見方が変わっているだけです。座標全体の向きや見方が変わっているため、測量座標の場合は、上で紹介した2つの公式が、

• sinθ×斜辺＝底辺（＝Y座標。sinでY座標が出ることは変わっていない）
• cosθ×斜辺＝高さ（＝X座標。cosでX座標が出ることは変わっていない）

に変わります。高さと底辺の位置が変わっているだけで、三角関数の公式に何か違いがあるわけではありません。測量座標になっても三角関数の公式はそのまま使えます。三角関数の公式を「sinθ×斜辺＝高さ」「cosθ×斜辺＝底辺」と覚えている方にとっては、高さと底辺の位置が逆になっているため、ややこしいと思いますが、「sinθを使う公式でY座標が求められ」、「cosθを使う公式でX座標が求められる」ことに関しては何も変わりがありません（そういう意味で測量座標になっても三角関数の公式はそのまま使えるということ）。要は三角関数の公式は最初から、

• sinθ×斜辺＝Y（高校の教科書風にいうと、sinθ＝y/斜辺）
• cosθ×斜辺＝X（同じく、cosθ＝x/斜辺）
• tanθ＝Y/X

と教えられていたほうが良かったかもしれないところを、数学座標はY軸が高さで、X軸が底辺になるため、

• sinθ×斜辺＝高さ（高校の教科書風にいうと、sinθ＝高さ/斜辺）
• cosθ×斜辺＝底辺（同じく、cosθ＝底辺/斜辺）
• tanθ＝高さ/底辺

という覚え方をさせられていたのです（たぶん。実際のところどうなのかは私には分かりません）。

ちなみに測量座標の縦（↑）のX軸から出発する角度（θ）のことは方向角と言います。そのため、このサイトでは座標値を求めるために使うこの公式のことを「方向角×斜辺」と呼んでいます。

---

この「方向角×斜辺」は、土地家屋調査士試験の過去問題集に載っているような一般的な座標値の求め方です。もし関数電卓の複素数モードという特殊な方法を使ってこの「方向角×斜辺」の計算をするなら「斜辺∠方向角」の形になります（∠は「SHIFT」「（ー）」で呼び出す）。

「方向角×斜辺」は順序を入れ替えて「斜辺×方向角」にしても答えが出ますが、「斜辺∠方向角」は順序を入れ替えることができません。入れ替えると正しい答えが出ません。

∠は何と読むかが分かりませんが、「かく」を変換すると出てきます。「斜辺∠方向角」は、最終的には最後の足し算も計算式に含めて「既知点＋斜辺∠方向角」の形で計算することになります。

---

とりあえず今は複素数モードという特殊な求め方のことは置いておいて、一般的な求め方、すなわち「方向角×斜辺」の計算をするときは、

• sin（方向角）×斜辺＝Y
• cos（方向角）×斜辺＝X

という公式を使います。そしてこの公式を使って点Eを求めるために、このページではまずは方向角を求めていこうと思います（どうして「方向角×斜辺」で点Eが求められるかが分からない方は、三角関数の公式で何を求めているかを理解できていない可能性があります）。

「方向角×斜辺」の公式を使って点Eを求めるために、このページではまずは点Aから点Eの方向角を求めていこうと思います。

• 四角形ABCDのうち角B、角C、角Dは角度が分かっている（75°、80°、90°）。
• 四角形の内角の和は360°のため、残りの角Aの大きさも分かる。360°－（75°＋80°＋90°）＝115°（←これが角A）

点B、点CはX座標が同じ（高さが同じ）、かつ角Bは75°のため、点Bから点Aの方向角（X軸と斜辺ABの挟角のこと）は、90°－75°＝15°になる。ちなみに角Aが115°ならその反対側の角度は245°です。

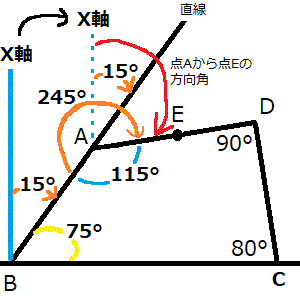
• トラバース計算により点Aから点Eの方向角を求める。15°＋（245°－180°）＝80°（←これが点Aから点Eの方向角）。

実は関数電卓の複素数モードを利用するなら点Aから点Eの方向角はもっと簡単に求めることができます。実際のところ本試験ではこちらの方法を使って問題を解くことになると思います。arg（D－A）。これだけで終わります。点Aから点Eの方向角を求めるのに、どうしてEではなくDを使っているかというと、座標値が分かっているのがAとDだからです。点Eは直線AD上にあるため、「点Aから点Eの方向角」と「点Aから点Dの方向角」はどちらも同じ値です。

AからDの方向角を求めるのに、どうしてかっこの中身が言葉の順番どおりに「A－D」にならずに「D－A」になっているかというと、arg（D－A）の前提として、原点から点Dの方向角を求める計算式、arg（D）が存在しているためです（次の画像を参照のこと。これはグラフの画像です）。

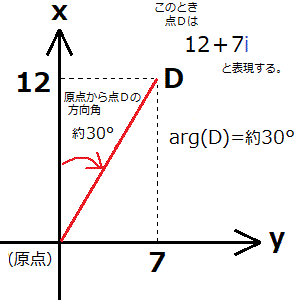
仮に点Dを（12，7）とすると、arg（D）すなわちarg（12＋7i）＝ほぼ30°となります（正確には30°15′23.17″です）。点Dを12＋7iと表現すること、iとは何なのか、12と7からどうやって30という数字を出しているかは、今はまったく気にする必要がありません。今ここで大事なのは、arg（D）で原点から点Dの方向角が分かるということです。

原点から点Dの方向角というのは、点Dが第1象限～第4象限のどこにあるかによって4つの形に分かれますが、いずれの形も原点（0.00，0.00）は常に同じ場所にあり、移動しておらず、その方向角を定める主導権は常にDが持っています（点Dの位置によってθが決まります）。そのため、原点から点Dの方向角を求める計算式はarg（D）なのです（次の画像を参照し、点Dの位置がθ（角度）を決めていることを確認のこと）。

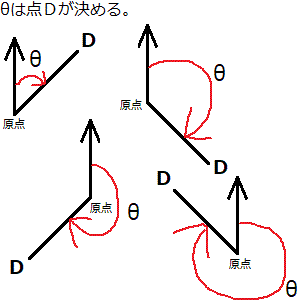
原点から点Dの方向角はarg（D）で求められます。しかし、土地家屋調査士試験で求めたいのは原点から点Dの方向角ではなく、点Aから点Dの方向角です。方向角の出発点が原点（0.00，0.00）ではないという違いがあるため、arg（D）では点Aから点Dの方向角を求めることができません（仮に点Aを（3，3）とすると、点Aから点Dの方向角は次の画像中のθのところです。次の画像中にもしarg（D）のことを書き加えるとしたら、どの点から出発してどの点が終点になる斜辺の線が引かれて、どこの角度がarg（D）のθになるかも、「arg（D）で求められる方向角」と「点Aから点Dの方向角」は「違う」ことを理解するために、一緒に確認しておいてほしいと思います）。

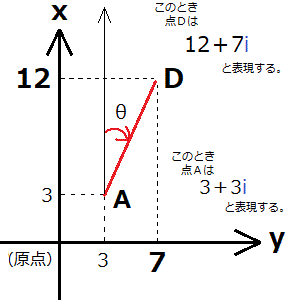
では、一体どうすればargを利用して点Aから点Dの方向角を求めることができるかというと、argが原点を前提とした計算式なら、辺ADが原点から伸びる線になるよう、辺ADを無理やり原点まで平行移動させてしまえば良いのです（次の画像を参照のこと）。

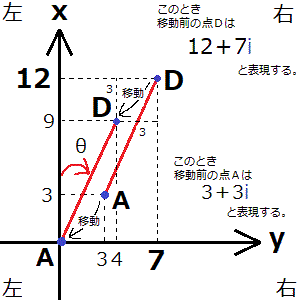
点Aを原点に持っていくために辺ADを下（↓）に3、左（←）に3だけ平行移動させる必要性から、arg（D）の計算式がarg（D－A）に変わります。その結果、arg（D－A）すなわちarg{（12＋7i）－（3＋3i）}＝arg（9＋4i）＝ほぼ24°となります。これが点Aから点Dの方向角です（A、Dに仮定の座標値を使って説明しているため、実際のH元年度の問題とは答えが異なるので念のため）。

もともとあった原点が前提の計算式arg（D）に、点Dが原点からの方向角ではない場合の例外として後から付け足されたのが－Aです。そのため、argの中身は「A－D」ではなく、「D－A」となり、arg（D－A）となるのです。

原点が前提の計算式arg（D）は、点Dに原点（0.00，0.00）の数字である0を足しても引いても何も影響がないため、arg（D）だけで良かったのです。arg{（12＋7i）－（0＋0i）}＝arg（12＋7i） ←何も変わってない！

ちなみにarg（D－A）の中身は常に「D－A」です。仮に点Aが（－3，－3）にあったとしても、「D＋A」になったりはしません。もし点Aが（－3，－3）にあったなら、点Aを原点に移動させるためには（＋3，＋3）が必要なのですが、仮に点Aが（－3，－3）にあったとしても、arg（D－A）すなわちarg{（12＋7i）－（－3＋（－3i））}＝arg{（12＋7i）＋3＋3i}となり、計算過程で（＋3，＋3）の形になるため、常にarg（D－A）で良いのです。

ただし、以上のすべてのことは、2016年度試験の受験会場で配布されていた早稲田法科専門学院のパンフレット「調査士午後試験 直前チェックポイント！」の「ポイント5 複素数による計算」に載っていた「方向角　arg（B－A）」という1行の計算式と、私が手持ちの三角定規と関数電卓を使ってつじつまが合うように勝手に考え出したもののため、私がここに書いていることが正しいことなのかどうかは私には分かりません。ネットで検索してみても原点が出発点になっている解説しか出てきませんが、「方向角　arg（B－A）」という計算方法があることは、予備校がそう言っているため確かです。2016年度試験の受験会場で配布されていた早稲田法科専門学院のパンフレット「調査士午後試験 直前チェックポイント！」の「ポイント5 複素数による計算」に載っていた計算式は次の通りです。

1. 座標計算 距離∠方向角
2. 辺長   abs（B－A）
3. 方向角  arg（B－A）
4. 面積   conjg（A）B＋…繰り返す

さて、ここからは具体的にarg（D－A）の関数電卓への打ち込み方を紹介したいと思います。次の①～④、このたった4つのことを覚えるだけでarg（D－A）が使えます。

① 関数電卓を複素数モードに変更する方法

まず関数電卓を通常計算モードから複素数モードに変更します。カシオのfxシリーズの関数電卓なら、右上のほうにある「ON」ボタンの隣の「MODE SETUP」ボタンを押し、次に「2」のボタンを押すと関数電卓が通常計算モードから複素数モードに変わります。

「MODE SETUP」「1」を押すと通常計算モードに戻ります。ただし、通常計算モードで行いたいことは複素数モードでもできるため、関数電卓は常に複素数モードにしておくと良いと思います。

② arg、iの表示方法

argは「SHIFT」「2」「1」で表示させます。点A（64.94，54.00）、点D（67.38，67.86）のとき、D－Aとなるarg（（67.38＋67.86i）－（64.94＋54.00i））＝80.015……となり、「°′″」ボタンを押すとその答えが角度に変換され、80°0′56.18″となり、これが点Aから点Dの方向角、ひいては点Aから点Eの方向角になります。なお、「i」は「ENG」ボタンで打ち込みます。関数電卓の「ENG」ボタンの右上に「i」という文字がプリントされていると思います。そのため「ENG」が「i」のボタンです（通常計算モードだと「ENG」ボタンは押しても何も反応がありません。何か計算をして「＝」を押した後なら反応があります）。

argを呼び出すのに「2」のボタンを使うというのは、なかなか覚えにくいことだと思います。関数電卓を複素数モードに変更する際にも「2」を使ったということで、同じ「2」のボタンを使っていることと関連させて覚えると良いと思います。

③ 点A、点Dの座標値をメモリーに保存する方法

試験では点A、点Dの座標値はメモリーに記憶させ、本当にarg（D－A）としか打たずに計算します。たとえば点Aなら 64.94＋54.00i と打ち込んだ後に「SHIFT」「STO」「A」と打つことでAメモリーに「64.94＋54.00i」を記憶させられます（RCLボタンのすぐ上にSTOと書いてあると思います。そのためRCLがSTOのボタンです。同じく、（－）ボタンの右上にAと書いてあると思います。そのため（－）ボタンがAのボタンです）。D点もこれと同じ要領でDメモリーに記憶させます。

Aの座標値をBのメモリーに、Dの座標値をCのメモリーに入れたりすることも可能ですが、座標値の英文字とメモリーの英文字が違っていると、どのメモリーにどの座標値を記憶させたかが分かりにくくなるため、座標値の英文字とメモリーの英文字は一致させたほうが良いと思います。

メモリーは計算モードを変更すると虚部のみ消える

記憶させたメモリーは別の計算モードに変更すると（たとえば複素数モードを通常計算モードに戻したりすると）虚部（iを付けた部分の数字）のみがクリアされます（消えます）。たとえば「12＋7i」と記憶させていれば「＋7i」の部分のみが消えます。「12」のほうは残りますが、「12」のほうが残っているからといっても虚部のほうは消えていますので、そのメモリーは再度電卓に入力し直さない限り、もう使い物になりませんので注意してください。

というのも、メモリーに記憶させた座標値は地積測量図に書く辺長を求める際に、たとえば辺ADの長さを求めるなら「SHIFT」「Abs」「A」「－」「D」「＝」というふうに再利用しますので、虚部が消えたことに気がつかないまま辺長の計算をしてしまうことがあるためです。

④ メモリーA、Dの呼び出し方

ここまで来てやっとarg（D－A）の計算式を作れます。メモリーは「ALPHA」ボタンで呼び出します。たとえばAのメモリーは「ALPHA」「A」で呼び出します。しふと、に、あーぐ、あるふぁ、でぃー、まいなす、あるふぁ、えー、かっことじ、いこーるです。これを心の中で呪文のように唱えながら一緒に電卓のボタンを押す練習をすると良いと思います。

私が使っている関数電卓（カシオのfxシリーズ）だと「ALPHA」は赤文字で書かれており、（－）ボタンの右上のAも赤文字で書かれています。これは要は関数電卓の赤文字の機能を利用するなら、その関数電卓の赤文字機能のボタンを押す前に「ALPHA」ボタンを押せ、ということだと思います。「SHIFT」ボタンもそのような使い方をするボタンになっています。

記憶させたメモリーの内容を確かめる方法

メモリーに記憶させた内容が何であるかを確かめたいときは「RCL」「A」、「RCL」「D」などと打つとAメモリーやDメモリーに記憶させた内容を見ることができます。

「RCL」はメモリーに数字を記憶させるために使った「STO」のボタンでもあったわけで、記憶させるために使ったボタンで、何を記憶させたかも確かめられるということで、両方とも同じボタンであることから、記憶させたメモリーの内容を確かめるボタンは比較的覚えやすいと思います。

「a＋bi」や「arg」は高校の数学Ⅲで学ぶ内容

「a＋bi」や「arg」は高校の数学Ⅲの内容で、複素数平面というところで学ぶそうです。土地家屋調査士試験で使う数学のうち高校でも習うのは数学Ⅰの三角関数、正弦定理、余弦定理、数学Ⅱの直線の方程式、内分点の計算、そして数学Ⅲの複素数平面です。高校で学ばない数学としてはトラバース計算や座標法などの測量関係の計算があります。

数学Ⅱの円の方程式を利用することで解ける問題もありますが（H11-E、H16-E。円の方程式で連立方程式を作る方法）、その方法だと計算時間がすごくかかりますし、普段は使わない公式のため、すぐに公式を忘れてしまって必要なときに思い出しにくいと思うので円の方程式を使うのはやめたほうが良いと思います。円の方程式を一度使ってみれば、少なくとも時間的にはこれではぜんぜん駄目だということがたぶん分かると思うので、一度確かめてみると良いと思います。

argはルートキーと同じようなものだと思えばよいと思います。ルートキーを使うと平方根が出ますが（たとえば2の平方根は1.41421356……です）、argを使えば角度が出ます。試験には制限時間があるため、平方根を筆算で出すのは時間的に厳しいと思います。角度もそうなのです。

---

次は「方向角×斜辺」の計算をするために使う斜辺（辺AE）を求めたいと思います。平成元年度の斜辺の求め方は2つあります。

ここからは「方向角×斜辺」の計算をするために使う斜辺（辺AE）を求めたいと思います。

• 問題文より、辺ABと辺EFは平行かつその間隔は2.20m。
• 四角形ABCDのうち角Aはこれまでの計算で角度が分かっており（115°）、さらに平行な2直線の間隔（2.20m）の意味が分かっていれば、角EAZ（下の画像中の赤いところの角度）が求められる（Zは問題文にはありません。私が勝手に置きました。これから赤いところの角度を求めていこうと思います）。
  
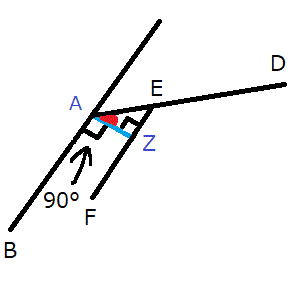
• 平行な2直線の間隔2.20m（上の画像中の青線。辺AZ）は、辺ABと辺EFに対して直角に交わる（これが平行な2直線の間隔の意味。「平行な2直線の間隔」と聞いただけでは、直角に交わらない線を引いてしまう方もきっと出てくると思いますが（そしてその線も確かに平行な2直線の間隔なのですが）、平成元年度の試験問題における平行な2直線の間隔（2.20m）というのは、辺ABと辺EFに対して直角に交わる線の間隔のことを意味しています。直角に交わる線なら直角に交わるものしか引けませんが、角度がどうでも良いなら、ほかにもいくらでも線を引けるため、平行な2直線の間隔を1つに特定するためには直角に交わる線を平行な間隔にするしかなかったのではないかと思います）。
• 直角は90°のため、角A115°－90°＝25°（←これが角EAZ。赤いところの角度）
• この角度と、平行な2直線の間隔2.20mを三角関数の公式に当てはめれば、辺AEが求められます。辺AEは三角関数の公式の斜辺に相当します。

平行な2直線の間隔の補足説明

平行な2直線の間隔2.20mの線分は、1か所にしか引けないものではありません（上の画像の青線のところだけが平行な2直線の間隔になるわけではない）。辺ABと辺EFに対して直角に交わる線分はすべて平行な間隔2.20mとなります。

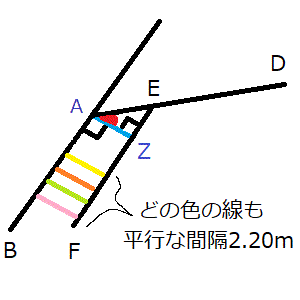
直角に交わる線でなければ平行な2直線の間隔を特定できないというのは、つまり、辺AB、辺EFに対して直角に交わる線でなくても、たとえば上の画像のいろいろな色の線は、もし辺AB、辺EFに対して直角に交わる線でなくても、すべて平行な2直線の間隔ではあるということです。極端なことを言えば点Aと点Fを結ぶ線分AFですら「辺AB、辺EFという平行な2直線の間にある線である」という意味では、平行な2直線の間隔です。

三角関数の公式

Yが高さで、Xが底辺になると考え、辺AEを求めます。

どうして「Yが高さで、Xが底辺になると考え、」なのかというと、私が三角形EAZをここではまだ数学座標の中にあるものとして考えているためです。私が思い描いているのは、次の画像中の数学座標のほうの三角形EAZです。私は測量座標よりも数学座標のほうに慣れているため、ここではまだ数学座標の三角形EAZを思い浮かべて斜辺を求めてみようと思います。

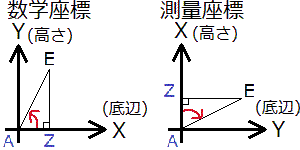
• sinθ×斜辺＝Y（数学座標なのでYは高さ）
• cosθ×斜辺＝X（数学座標なのでXは底辺）

sinθを使う問題でY座標が求められ、cosθを使う問題でX座標が求められるという意味では三角関数の公式は1つしかありませんが、sinθ＝高さ/斜辺、cosθ＝底辺/斜辺という覚え方をしているなら数学座標と測量座標とで高さと底辺の位置が入れ替わっているため、あたかも三角関数の公式が2種類あるかのように見えるのではないかと思いますが（測量座標ならsinθ＝底辺/斜辺、cosθ＝高さ/斜辺になる）、三角関数の公式が2種類あるとは思えませんので、やはり三角関数の公式はsinθを使う公式でY座標が求められ、cosθを使う公式でX座標が求められるという意味で1つしかないものだと思っておいたほうが良いのではないかと思います。

式の作り方

分かっている情報を公式（「？」「？°」×斜辺＝「？」）の中に当てはめていきます。

• ①. 角EAZ（赤いところの角度）は25°
  • 「？」「25°」×斜辺＝「？」

• ②. 分かっている斜辺ではない辺の長さは2.20
  • 「？」「25°」×斜辺＝「2.20」

• ③. この2.20は数学座標なら底辺なので、求めるときにcosを使う。
  • 「cos」「25°」×斜辺＝「2.20」

もし三角形EAZを測量座標の中にあるものとして考えるなら、③.のところが「この2.20は測量座標ならX軸なので、求めるときにcosを使う」になります。思い描いているグラフや図形が違うだけで結論は同じです。

計算する

cos25°×斜辺＝2.20

（cos25°は真数表に載っている）

0.906×斜辺＝2.20

斜辺×0.906＝2.20

斜辺＝2.20÷0.906

斜辺＝2.428……（←これが辺AE）

「方向角×斜辺」の計算をするために使う斜辺（辺AE）は次の方法で求めることもできます。

• 四角形ABCDのうち角Aの角度（115°）が分かっていれば、角XAEの角度が求められる（Xは問題文にはありません。私が勝手に置きました）。半円は180°のため、180°－115°＝65°（←これが角XAE）
  
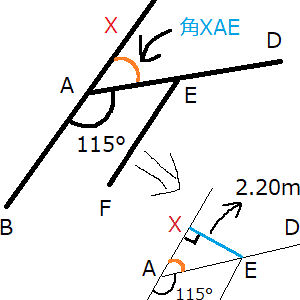
• 平行な間隔2.20mの直線（上の画像中の青線）で三角形XAEを作る。
• 三角関数の公式で辺AEが求められる（辺AEは斜辺に相当する）。

三角関数の公式

三角関数の公式を使って辺AEを求めます。今回は試しに三角形XAEを測量座標の中にあるものとして考えてみようと思います。

• sinθ×斜辺＝Y
• cosθ×斜辺＝X

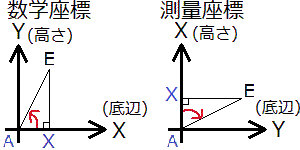
式の作り方

分かっている情報を公式（「？」「？°」×斜辺＝「？」）に当てはめていきます。

• ①. 角XAEは65°
  • 「？」65°×斜辺＝「？」

• ②. 三角形XAEのうち、長さが分かっている斜辺ではない辺の長さは2.20m。この2.20mは測量座標ならY軸の大きさのため、求めるときにsinを使う。
  • 「sin」65°×斜辺＝「2.20」

これで式は完成しましたが、ここで1つ問題が生じます。それは問題用紙の真数表に65°の値が載っていないことです。そのため65°を別の角度に変換しなければなりません。ただし、関数電卓を使って問題を解くなら、sin（65°）やcos（65°）と打てば関数電卓がそれを勝手に真数に直して計算してくれるため、角度の変換は必要ありません（打つのが度（°）だけなら「°」の記号は省略可。分（′）まであるときは、°や′の記号が要る。秒（"）まであるときは、°′"の全部の記号が要る）。

角度の変換

65°の三角形は数学座標なら次のような形をしています。そして、そのsin（y座標。数学座標なら高さ）はオレンジ色の線のところです。

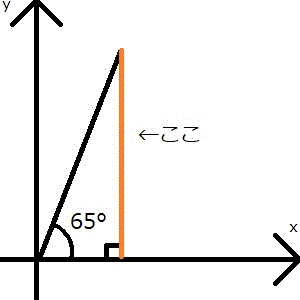
要はこのオレンジ色の線と同じ長さを、別の角度で表せば良いのです。下の画像を見てください。65°の三角形の反対側には25°の三角形が作れます。そして、その三角形の黄色の線と、65°の三角形のオレンジ色の線は長さが同じです。

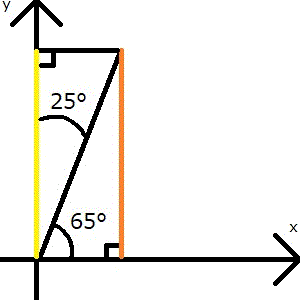
この25°の三角形の角度をきちんとx軸から出発させると次のようになります。

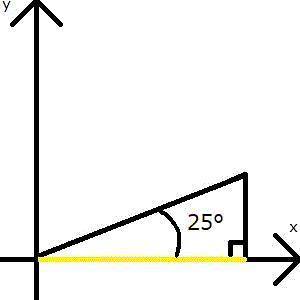
黄色の線は25°の三角形のx座標（cos。数学座標の底辺）に相当します。つまり「65°の三角形の高さ」＝「25°の三角形の底辺」です（要はsin65°＝cos25°です）。そしてcos25°なら問題用紙に真数表が載っています。

辺AEを求める

sin65°×斜辺＝2.20

sin65°は変換するとcos25°（cos25°は真数表にある）

0.906×斜辺＝2.20

斜辺×0.906＝2.20

斜辺＝2.20÷0.906

斜辺＝2.428……（←これが辺AE）

あとはこれまでに求めた「点Aから点Eの方向角」と「斜辺AE」の数値を下の三角関数の公式に当てはめ、そこで得られたX座標とY座標を、点AのX座標とY座標に加えれば、答えとなる点Eの座標値が求められます。

• cosθ×斜辺＝X座標（＝測量座標の高さ）
• sinθ×斜辺＝Y座標（＝測量座標の底辺）

この三角関数の公式の答えをどうして点Aに加えるかが分からないなら、三角関数の公式で何を求めているかを理解できていない可能性があります。「cosθ×斜辺＝X」で下の画像中の①の辺の長さが求められ、「sinθ×斜辺＝Y」で下の画像中の②の辺の長さが求められます。そのため、未知の点Eを求めるためには、この①と②の距離をそれぞれ点AのX座標、Y座標に加える必要があるのです。

②の線は点Aから線が伸びていないため、人によっては点Aからの距離であることが分かりにくいと思います。点Eから真っすぐ下に線を下ろして、③の線は点Aから出ていることを確認した後、③の線の長さと②の線の長さはどちらも同じ長さであることを確認してください。

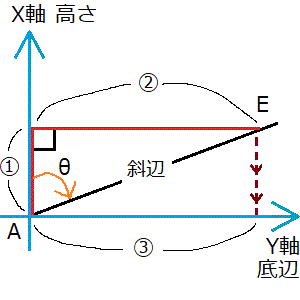
「方向角×斜辺」の答えを点Aに足すことを思うと、どうしてθが方向角でなければならなかったかも分かると思います。下の画像の例で言うと、赤の三角形の高さと底辺を点Aに足せば点Bの座標値が求められますが（点Aから上に1個、右に2個動いたところに点Bがあることが分かりますが）、青の三角形の高さと底辺を点Cに足しても点Dの座標値は求められません。青の三角形は高さと底辺が斜めになっているためです。

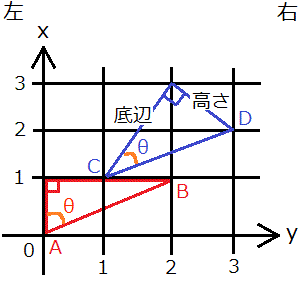
ちなみに上の画像の赤の三角形と青の三角形は、斜辺の長さは同じです（辺ABと辺CDは同じ長さ）。そのため、青の三角形を利用して求めた斜辺を、赤の三角形の斜辺として利用することはできます。この年の問題で使った「方向角×斜辺」の斜辺も、その仕組みを利用して求めています。

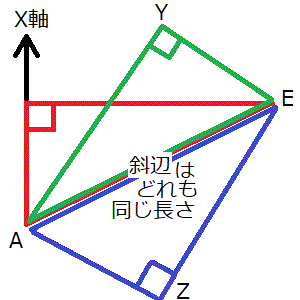
三角形AEZ（青の三角形）が「斜辺（辺AE）を求める式（1つ目）」で使った三角形で、三角形AYE（緑の三角形）が「斜辺（辺AE）を求める式（2つ目）」で使った三角形です。

点Eは内分点の公式 or 比の計算で求めることもできます。筆算でルートを開くのは大変なので、ルートキー付きの電卓がないと、この方法は使いにくいです。

---

2010年代の中頃以降、コンビニの電卓からルートキーがなくなり、その代わりに税込、税抜という税率計算のボタンが付くようになりましたが、100円ショップの電卓にはまだ（2026年現在）ルートキーが付いています。もし土地家屋調査士試験を受けるならそろばんやコンビニの電卓を使うよりもルートキーが付いている100円ショップの電卓がおすすめです。

---

これまでの計算で、すでに辺AEの長さは求められており、さらに点A、点Dは測量成果により座標値が分かっているため、三平方の定理により辺ADの長さを求めると、内分点の公式 or 比の計算により点Eを求められます。

内分点の公式 or 比の計算のどちらで問題を解くにしろ、まずはピタゴラスの定理（三平方の定理とも呼ばれる）か関数電卓の複素数モードを使って辺ADの長さを求める必要があります。

ピタゴラスの定理（三平方の定理とも呼ばれる）

• 斜辺＝√（高さ²＋底辺²）

これで辺ADの長さを求める。この式はよく見るピタゴラスの定理「高さ²＋底辺²＝斜辺²」を電卓に打ち込みやすいように変形したものです。「斜辺＝」の後の「√（高さ²＋底辺²）」の部分を電卓に打ち込みます。

関数電卓の複素数モードを使って斜辺を求める方法

関数電卓の複素数モードを利用するなら「SHIFT」「Abs」「A」「－」「D」「＝」でも斜辺を求められます。通常の方法と比べてボタンを押す回数が少なくなるため計算時間を短縮でき、また、（ボタンを押す回数が少なくなるわけですから）打ち損じを発生させるタイミングを減らすこともできるため、斜辺を求める際にはこちらの方法を使ったほうが良いと思います。

方向角を求める計算式arg（D－A）のときと違って、辺ADを求めるときの「A」と「D」の順序はどちらを先にしても良いです。これはこの計算で出る答えが絶対値のためです。「SHIFT」「Abs」と打つと関数電卓の画面に|□|と表示されますが（そしてこれから□の部分にメモリーに記憶させたAとDを入れるのですが）、たぶんこの||は絶対値の記号だと思います。「1－4」と「4－1」の答えの絶対値はどちらも3です。そのため、たとえば辺ADを求めるときの「A」と「D」の順番はどちらを先にしても良いのです。

比の計算

「ピタゴラスの定理」か「関数電卓の複素数モード」で求めた斜辺を使って比の計算をします。

測量士補試験の地形測量の問題を解くときに使ったのと同じ方法です。辺ADが辺AEのように縮むなら、高さや底辺はどのように縮むかという計算をします。比の計算が使えるときは、次に紹介する内分点の公式でも問題を解けることが多いですし、その逆もまたしかりです。内分点の公式で問題を解けるときは、比の計算でも問題を解けることが多いです。

内分点の公式

「ピタゴラスの定理」か「関数電卓の複素数モード」で求めた斜辺とこれまでに求められている辺AEの長さを利用して辺DEの長さを求め、内分点の計算をします。

• {（AのX座標×辺DEの長さ）＋（DのX座標×辺AEの長さ）}÷辺ADの長さ＝EのX座標
• {（AのY座標×辺DEの長さ）＋（DのY座標×辺AEの長さ）}÷辺ADの長さ＝EのY座標

内分点の公式は文字で見るよりも実際に関数電卓に打って計算してみたほうが分かりやすいです。卓球のラリーのようにポンポンと行ったり来たりする計算になっていると思います。関数電卓ではなく普通の電卓を使うなら、たぶん電卓にカッコが打てないと思うのでこの公式は使いにくいです。土地家屋調査士試験を受けるなら100円ショップの電卓を使うよりも関数電卓がおすすめです。

関数電卓の複素数モードを使って内分点の計算をする方法

もしかすると内分点の計算は、関数電卓の複素数モードを使うなら（メモリーA×反対の辺＋メモリーD×反対の辺）÷辺AD＝でX座標、Y座標が同時に出るのではないかと思います。

点Eは直線の方程式で求めることもできます。辺ADを通る直線と辺EFを通る直線の交点が点Eになります。直線の方程式に関しては、それを使わないと解けない別の年度の問題（たとえば平成2年（1990年）度のF点）で詳しく説明しています。

---

ここでも少し説明しておくと、まず「辺ADを斜辺に持ち、90°が左側（←）にある直角三角形」からtanθを求めます。「tanθ＝高さ/底辺」より、「tanθ＝13.86÷2.44＝5.6803……」。このtanθと点Aの座標値を利用して直線ADの方程式を作ると、y＝5.6803（x－64.94）＋54。

次に直線EFの方程式を作ります。辺ADと辺EFは平行で、点Bと点Cは同じ高さにあり、角Bが75°のため、角FPGは75°であることが分かり、点Fから点Eの方向角は「直角90°－75°＝15°」であることが分かります。

「tanθ＝sinθ/cosθ」より、「tan15°＝sin15°/cos15°＝0.258÷0.966＝0.2670……」（15°のsinとcosは真数表に載っています）。このtan15°と点Fの座標値を利用して直線EFの方程式を作ると、y＝0.2670（x－52.78）＋53.02。

あとはこの直線ADの方程式と直線EFの方程式をつなぐと答えが出ます（どちらの直線の方程式も「y＝」のため、一方の直線の方程式を、もう一方の直線の方程式に代入できる）。

---

なお、CASIOの関数電卓（私が持っているのはfxシリーズ）を使うなら「MODE SETUP」「5」「1」で連立方程式を作って交点を求めることもできます。実際のところ本試験ではこちらの方法を使って問題を解くことになると思います（ただし、モードを変更することになるため、もしメモリーに虚部を記憶させているならそれが消えます）。連立方程式の答えが交点です。その際は直線の方程式の公式を「y＝tanθ（x－通るx）＋通るy」と覚えずに「tanθx－y＝tanθ通るx－通るy」と覚えたほうがイコールの前後が同じ形で覚えやすいし、関数電卓に数字を打ち込みやすくなるので良いと思います。

とはいえ、tanθが90度だったりすると「tan90°＝なし」のためエラーが出て「MODE SETUP」「5」「1」で連立方程式を作る方法が使えないため、普通の一般的な形のほうの公式も覚えておかざるを得ず、普通の公式と関数電卓用の式とではYのプラス、マイナスが逆になっているため、ややこしいところもあると思います。と思いきや、実はtan（90）をtan（90.0001）などと打ち込むことで、「MODE SETUP」「5」「1」で連立方程式の計算をすることができるようです。ただし、小数点以下の0の数はそろえなければなりません。1行目の式も、2行目の式も、どちらも小数点以下0の数をそろえなければなりません（要は同じ数字を使わないといけない）。大事なのは0の数をそろえることであって、同じ数字であれば「90.01」（小数点以下の0が1個）を使っても、「90.001」（小数点以下の0が2個）を使っても答えは出ます。小数点以下の0が0個の「90.1」でも答えが出るくらいです（H16-21で確認）。