【土地家屋調査士試験】
平成2年（1990年）度

点D、点Cは測量成果により座標値が分かっており、さらに見取図には辺DGの長さが載っているため、三平方の定理により辺DCの長さを求めれば、内分点の公式 or 比の計算により点Gの座標値を求められる。

平成元年度「E点」と同じ問題です。

測量成果によるとA点、B点は高さが同じ（X座標が同じ）。したがって、その直線上にあるE点のX座標もそれと同じ。また見取図には点Aから点Eまでの距離が載っており、点AのY座標にその距離を足すことで点EのY座標を求められる。

直線の方程式で求めます。直線GFと直線FEの交点がF点です。

直線の方程式

点（x，y）を通り、傾きがθの直線は、次のような方程式で表すことができます。

• y＝tanθ（x－通るx）＋通るy

測量座標のため、tanθのθには方向角を使います。

直線GFの方程式

まずは辺GFの方程式を作ります。ちなみに下の画像中のX、Y、Z（赤字の英文字）は問題文にはありません。解説のために私が勝手に置きました。

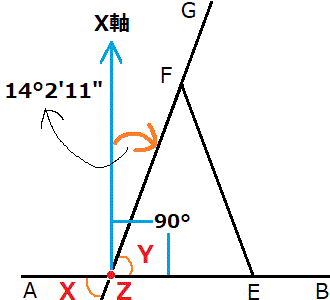
問題用紙掲載の見取図によると角Xは75°57′49″のため、その対頂角である角Yも同様の角度であることが分かります。そして点Aと点BはX座標が同じ（要は高さが同じ）ため、点Zから点Fの方向角は、直角90°－角Y（75°57′49″）＝14°2′11″であることが分かります。これが傾き（tanθ）になります。そして辺GFの直線は既知の点G（58.57，43.38）を通ります。これが公式の中の「通るx」「通るy」になります。したがって、直線GFの方程式は

• y＝tan14°2′11″（x－58.57）＋43.38

となります。

直線FEの方程式

問題用紙掲載の見取図に角FEBの大きさが載っています（106°41′57″です）。106°41′57″－直角90°＝16°41′57″ですが、この角度は方向角とは逆向きに進んでいるため、頭にマイナスを付けて「－16°41′57″」とします。これが直線FEの傾き（tanθ）です。そしてこの直線は既知の点E（40.00，41.00）を通ります。これが公式の中の「通るx」「通るy」になります。したがって、直線FEの方程式は

• y＝tan（－16°41′57″）（x－40.00）＋41.00

となります。

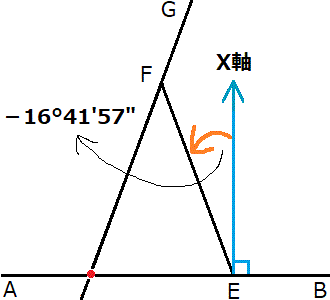
ちなみにこのマイナスの方向角に360°を足せば、方向角をプラスの角度に直すこともできます。tan（－16°41′57″）＝tan343°18′3″です。

tanθは幾らか

しかし、ここで1つ問題が生じます。それは真数表にtanの値が載っていないことです。そのため、tanは自力で求める必要があります。

三角関数の公式には次のようなものがありました。

• tanθ＝高さ/底辺

実はこの公式には続きのようなものがあり、

• tanθ＝高さ/底辺＝sinθ/cosθ＝y/x

となります。

要はtan14°2′11″は、

• tan14°2′11″＝sin14°2′11″/cos14°2′11″

となります。

角度の変換

しかし、ここでまた1つ問題が生じます。それは真数表にsin14°2′11″、cos14°2′11″の値が載っていないことです。そこで角度を変換します。

• sin14°2′11″（θ＝14°2′11″の三角形の高さ）＝cos75°57′49″（θ＝75°57′49の三角形の底辺）
• cos14°2′11″（θ＝14°2′11″の三角形の底辺）＝sin75°57′49″（θ＝75°57′49の三角形の高さ）

したがってtan14°2′11″は次のようになります。

• tan14°2′11″＝sin14°2′11″/cos14°2′11″＝cos75°57′49″/sin75°57′49″

75°57′49″は真数表にsinとcosの値が載っているため、tan14°2′11″＝0.243÷0.970＝0.2505154639……であることが分かります。

---

そのため、直線GFの方程式は最終的にはy＝0.2505（x－58.57）＋43.38となります。

同様に直線FEの方程式を求めると、y＝－0.2995（x－40.00）＋41.00となります。tan（－16°41′57″）＝sin（－16°41′57″）/cos（－16°41′57″）＝cos106°41′57″/sin106°41′57″＝－0.287÷0.958＝－0．2995……。これが傾きになります。

連立方程式

直線GFと直線FEの交点が点Fです。交点は連立方程式で求めます。tanθは小数第4位まで使わないと答えがズレます。

• y＝0.2505（x－58.57）＋43.38……①
• y＝－0.2995（x－40.00）＋41.00……②

①の式のyのところに②を代入して（どちらも同じyのため代入できる）、

• －0.2995（x－40.00）＋41.00＝0.2505（x－58.57）＋43.38

これを解けばF点のX座標を求められます。F点のX座標が分かれば、今度はそれを①か②のどちらかの式（どちらでも良いです）のxに代入すればF点のY座標を求められます。