【土地家屋調査士試験】
平成元年（1989年）度「G点」「F点」

• 測量成果によると点B、点CはX座標が同じ（要は高さが同じ）。したがって、その直線上にある点Gの高さは点B、点Cの高さに等しい。

---

土地家屋調査士試験の受験生は、自分で測量をしたわけでもなく誰かが勝手に作成して突然自分が見ることになった測量成果から点B、点Cが同じ高さになることを一瞬で見抜かなければなりません。

G点のY座標を求めるためには、辺BP（①の辺）と辺PG（②の辺）の長さを求め、既知点BのY座標にそれらの長さを足す必要があります。

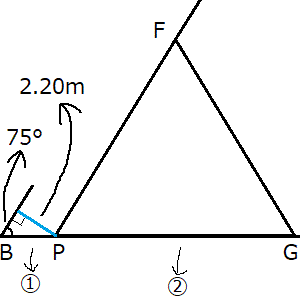
辺BP（①の辺）の求め方

平行な間隔2.20mを利用して直角三角形を作り、Yが高さで、Xが底辺になる数学座標の三角関数の公式を使って求めます（私は数学座標のほうに慣れているため）。

• sinθ×斜辺＝高さ
• cosθ×斜辺＝底辺

式の作り方

分かっている情報を公式（「？」「？°」×斜辺＝「？」）に当てはめていきます。

• ①θは75°
  • 「？」75°×斜辺＝「？」

• ②高さ（数学座標ならY座標。つまりsin）は2.20m
  • 「sin」75°×斜辺＝「2.20」

計算する

sin75°×斜辺＝2.20

sin75°＝cos15°のため、

cos15×斜辺＝2.20

斜辺×cos15＝2.20

斜辺＝2.20÷0.966

斜辺＝2.277……（←これが辺BP）

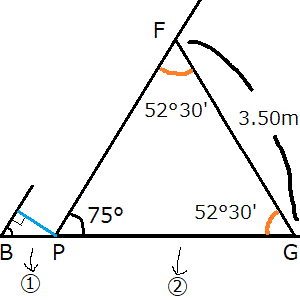
辺PG（②の辺）の求め方

• 問題文の注意事項により、辺FGは3.50mかつ辺FPと辺GPは同じ長さ。
• 辺ABと辺EFは平行かつ点B、点Cは高さが同じ。したがって角FPGも75°であることが分かる。
• 三角形の内角の和180°－角FPG75°＝105°。三角形FPGは二等辺三角形のため、この105°を2で割ったものが三角形FPGの角F、角Gの角度になる。
• 105°÷2＝52°30′（←角F、角Gの角度）

正弦定理

2つ以上の角度と1つの辺の長さが判明しているため、正弦定理で辺PG（②の辺）が求められます。

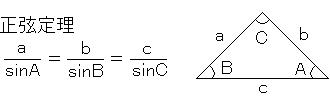
3.50/sin75°＝X/sin52°30′

X＝2.873……（←これが辺PG）

G点のY座標

B点のY座標（50）＋辺BP（2.277……）＋辺PG（2.873……）＝55.15……です。

三角形FPGは二等辺三角形のため、辺PGが2.873……mなら辺PFも2.873……mです。点Pから点Fの方向角は15°です（直角90°－75°＝15°）。あとは「方向角×斜辺」をすれば点Fの座標値を求められます。