三角関数の基礎知識

• sinθ×斜辺＝高さ

  サンシャイン。高くそびえる高層マンションをイメージして。

• cosθ×斜辺＝底辺

  コストパフォーマンスを気にする底辺。門地（生まれ）が良くなくて貧乏なので。

θで何がしたいのかというと、足のつま先を右に向けて立っている人が見ている木の高さや、その木までの距離（底辺の長さ）が知りたいのだと教科書ではよく言われていたと思います。ここでは木で説明していますが、もしこれが木ではなくて山だったり坂道だったりしたら、山の頂上までの距離や坂の上に行くまでの距離を求めることもできます（斜辺がそれに該当する。上に書いた2つの公式をそれぞれ変形させると、斜辺＝高さ÷sinθ、斜辺＝底辺÷cosθになる）。

斜辺を求める式への変形の仕方の覚え方

←左 右→

たとえば「sinθ×斜辺＝高さ」であれば、

1. sinθ×斜辺＝高さ （ここから変形開始）
2. 斜辺×sinθ＝高さ （交換法則を満たすため、sinθと斜辺は入れ替えられる）
3. 斜辺＝高さ÷sinθ （2.の式の「×sinθ」を移項して「÷sinθ」にする。2.の式の左項（←）にある「×sinθ」を消すために、左右両方の項に「÷sinθ」を付けて計算すると、左項（←）の「×sinθ」が約分されて消えて、右項（→）の「÷sinθ」だけが残るためそうなる）

となります。

←左 右→

これは年寄りの私が変形後の式の形を忘れたときに、その式の形を思い出すための方法です。この変形の仕方に限らず、私がこのページに書いていることが正しいことなのかどうかは私には分かりません。

公式の覚え方（その2）

アルファベットのSとCを使うと次のようにして公式を覚えることもできます（アルファベットのtで公式を覚えられるtanθはおまけです。測量士補試験はtanθはほとんど使いません）。一見、上で紹介した公式とは違う別物に見えるかもしれませんが、ただ式を変形しているだけなので、使うのはどちらでも構いません（「2×3＝6」を「2＝6/3」にしているようなものです。6/3は分数です。3分の6と読みます。6月3日のことではないです。素直に順番通りに6÷3と理解したほうが順番通りで読みやすくなると思います）。

高校の教科書に載っている公式

• sinθ＝高さ/斜辺 （斜辺ぶんの高さ、と語順を逆にして読みます。要は「高さ÷斜辺」です）
• cosθ＝底辺/斜辺 （斜辺ぶんの底辺。要は「底辺÷斜辺」です）
• tanθ＝高さ/底辺 （底辺ぶんの高さ。要は「高さ÷底辺」です）

tanθについては「高さ」が分数の上側（分子）で、「底辺」が下側（分母）になっており、見た目と文字が一致しているので覚えやすいと思います（高さ→高い→上側。底辺→底→下側）。測量士補試験ではtanθの公式は使いませんが一応。

どこがθか

この公式の中の、たとえば「cosθ」のθがどこの角度のことなのかは直感で分かると思います。30°のところをCで囲っていますからね。しかし「sinθ」と「tanθ」のθはそうはいきません。たとえば上の画像の三角形のSのところを見ると、斜辺と高さに挟まれている60°のところが「sinθ」のθではないかと勘違いしてしまうのではないでしょうか。しかし、このときに「sinθ」のθがどこの角度のことなのかというと、60°のところではなくて30°のところなのです。θは常に人間が立っている場所の角度です。

sin30°やcos30°と聞くと、その語順から「sinの30度」と「cosの30度」の2つの30度があると勘違いしがちですが、実はそうではなく「30度のsin」「30度のcos」と考えたほうが分かりやすいです。2つの30度があるのではなく、1つの30度の中にsinとcosの2つがあります（測量士補試験では使わないのでここでは省略していますが、もちろん1つの30度の中にはtanもあり、要は1つの30度の中にはsin、cos、tanの合計3つがあります）。θが30度の三角形の高さ/斜辺がsin30°で、θが30度の三角形の底辺/斜辺がcos30°です。

そのため、高校の教科書に載っている公式は、

• sinθ＝高さ/斜辺
• cosθ＝底辺/斜辺
• tanθ＝高さ/底辺

となります。

1つ上の公式の作り方（アルファベットを使う方法）は、人が足のつま先を右に向けているときにしか通用しません。たとえば木が左に生えているからと言って、人が左を向いていたらどうなるか（90°が左側に来る直角三角形を書いてSやCを当ててしまう人もきっといると思います。直角三角形にSやCを当てることは有名ですが、その直角三角形が「90°が右側に来る直角三角形」でなければならないことに関してまで言及している人は少ない（というかほぼいない）と思います）。

人が左を向いているときにSやCを使うと、次のような公式を作ることになります。しかし、この公式は間違っています。底辺と高さの位置が逆です。

↓間違い↓

• sinθ＝底辺/斜辺
• cosθ＝高さ/斜辺

ここで問題なのは、あくまでも人が左を向いているところです。木が左に生えていることは問題ではありません。右を向いて立っている人でも、体を後ろに反らせば左に生えている木を見ることができます（sinθが90°を超えるときの画像を参照のこと）。

たとえば次の画像の中の点Pのx座標（？の部分の長さ）を求めたいときは、三角形の向きを次のように変えて考えます。画像が小さくて書けなかったのでここに書きますが、この三角形の原点（0）のところの角度は30°とします。すると当然、点Pのところの角度は60°ですね（三角形の内角の和は180°なので）。

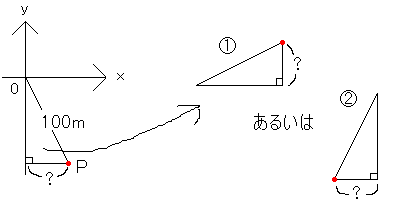
①のときは高さを求めたいので、サンシャインより、
   sin30°×100m
    ＝0.5×100m
    ＝50m

②のときは底辺を求めたいので、コストパフォーマンスを気にする底辺より、
   cos60°×100m
    ＝0.5×100m
    ＝50m

念のために再度書いておきますが、θは人間が立っている場所の角度です。そして人は足のつま先を右に向けて立っています。

測量士補試験は問題用紙の巻末に関数表が載っているので、これを覚えておかないと答えが出ないということはないと思いますが、これを知っていると問題を解くときにごくまれに便利だと思うことがあります。θの位置は人が立っているところ（青色のところ）です。1：2：√3、1：1：√2の直角三角形にアルファベットを当てて覚えます。たとえばsin30°の三角比は1/2です。cos30°の三角比は√3/2です。tanθについては三角比どころか、関数表を参照することも滅多にありませんが一応。

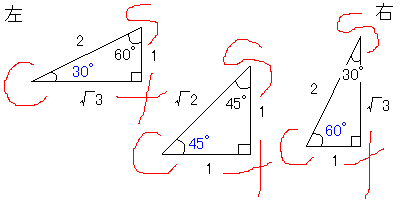
2＝√4＞√3です。そして三角形の3つの辺の中では斜辺が一番長いです。2と√3で位置を迷う人がいるかもしれないので一応。

三角形が直角三角形のときは「斜辺²＝高さ²＋底辺²」が成り立ちます。たとえば1つ上の画像の一番左の三角形の数字をこの公式に当てはめたときは「（2）²＝（1）²＋（√3）²」です。もう一度書きますが、この公式は直角三角形のときにしか使えません。直角三角形とは90°の角度を持つ三角形のことです。直角三角形の斜辺の求め方には他にも次のような方法があります。

斜辺²＝高さ²＋底辺²－2×高さ×底辺×cos90°

「斜辺²＝高さ²＋底辺²」は直角三角形のときにしか使えませんが、「斜辺²＝高さ²＋底辺²－2×高さ×底辺×cos90°」の公式を使うときは、直角三角形でなくとも斜辺の長さが求められます。90°のところを他の角度に変えれば良いのです。偏心補正計算をするときはごく稀に、この「a²＝b²＋c²－2bc cosA」という公式（余弦定理）を使うことがあります（リンク先は正弦定理の問題ですが……）。

ちなみに「sinθ＝高さ/斜辺」というのは、直角三角形のときの正弦定理（a/sinA＝b/sinB＝c/sinC）です。たとえば1つ上の画像の一番左の三角形はsin30°＝1/2ですが、この三角形を正弦定理に当てはめると2/sin90°＝1/sin30°となり、sin90°は1ですから、2＝1/sin30°となり、ここから式を変形して形を整えると、sin30°＝1/2となります。sinθ＝高さ/斜辺と同じ形です。

ちなみにこれは測量士補試験とは関係のない公式の話ですが、「sinθ²＋cosθ²＝1」という公式を大昔に高校で習った覚えがありますが、もしかするとこれはピタゴラスの定理と同じく、高さ²＋底辺²＝1ということなのかもしれません。一応念のために書いておきますが、このページの内容はすべて測量士補試験の勉強中に私が勝手に思いついたことを書いているだけなので、ここに書いてあることが正しいことなのかどうかは私には分かりません。

関数表に載っているsinとcosの値は90°までですが、偏心補正計算の問題を解くときは、まれに90°を超えるsinθの値が必要になることもあります。そんなときは「180°－θ」でsinθの値を90°未満に直しましょう。たとえばsin120°は、「180°－120°」でsin60°になります。

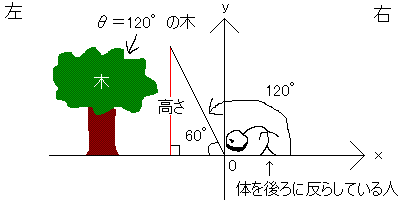
sinθ＝y座標（＝高さ）と考えると分かりやすい（斜辺が1のときはそうなる。意味がよく分からない人は一番上の公式やアルファベットで作った公式の斜辺のところに1を代入してみて。たとえば3/1（1分の3。要は3÷1）は3ですよね。分母が1のときはそれを省略できるので。ということは「sinθ＝高さ/斜辺」の斜辺に1を代入するとsinθ＝高さになりますよね。そして高さは数学座標だとy座標ですよね）。θ＝120°の木の高さは、θ＝60°の木の高さと同じです。木が立っている場所が違うだけです。θ＝60°の木は右に立ちます（三角比の画像の中の一番右の三角形がθ＝60°の三角形です）。

測量士補試験には必要のない知識ですが、θが180°を超えるときは別の式を使ってθを90°未満に直すことになります。考え方は上の画像と同じです。体の柔らかい人が思いっきり体を反らして地面にめり込みます。

測量士補試験にはいらない知識です（少なくとも私が勉強していた頃は必要なかった。今でも使わないかどうかは私には分かりません）。cosθが90°を超えるときは－（180°－θ）になります。たとえばcos120°は、－（180°－120°）で－cos60°です。

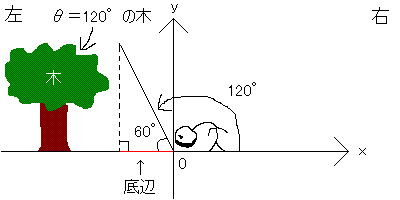
cosθ＝x座標（＝底辺）と考えると分かりやすい（斜辺が1のときはそうなる）。θ＝120°の底辺（木までの距離）は、θ＝60°の底辺（木までの距離）と同じです。ただし、θ＝120°のほうは木が後ろ（グラフを4分割したときの左上（↖）の場所。ここは「第二象限」と言われる場所です。原点が0のときに高さはプラス、底辺はマイナスになる場所です）に生えているので頭にマイナスが付きます。この求め方もθが180°を超えたときは使えなくなります。

たとえばθ＝210°のときのイメージは次の通りです。

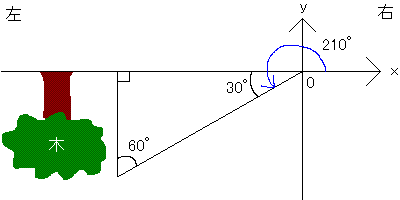
θが210°のときの木の高さ（sin）は、θが30°のときの木の高さと同じです。でもθが210°のときは、木が下に向かって生えているので頭にマイナスが付きます。つまりsin210°＝－sin30°です。

θが210°のときの木までの距離（底辺、cos）は、θが30°のときの木までの距離と同じです。でもθが210°のときは、木が左のほうに生えているので頭にマイナスを付けます。つまりcos210°＝－cos30°です。

グラフを4分割したときの左下（↙）の場所は「第三象限」と言われる場所です。ここは原点を0としたときに高さはマイナス、底辺もマイナスになる場所です。

注意事項（兼このページの大事なこと3つのまとめ）

• θは人が立っているところの角度（大事なのは上から4番目の小見出しの「どこがθか」のところです）。
• 人は足のつま先を右に向けて立っている。
• 木は地面から生える。←new！！
  （図を描くときに木をy軸から生やしたら駄目って意味です。θが270°を超えたときも同じです。木は全部地面から生えます）

ところで土地家屋調査士試験の合格者の約5割を輩出している資格予備校やフルカラーテキストの調査士講座のことをご存じでしょうか？ 当サイトおすすめの土地家屋調査士試験、測量士補試験の予備校講座はこちらです。リンク先で詳細をご確認下さい。