当サイトはアフィリエイトプログラムを利用して商品の紹介を行っています。
偏心補正計算の問題
試験問題 2014年度 No.6
図6のように、既知点Bにおいて、既知点Aを基準方向として新点C方向の水平角を測定しようとしたところ、既知点Bから既知点Aへの視通が確保できなかったため、既知点Aに偏心点Pを設けて、水平角T´、偏心距離e及び偏心角φの観測を行い、表6の結果を得た。既知点A方向と新点C方向の間の水平角Tは幾らか。
ただし、既知点A、B間の距離Sは、2,000mであり、S及び偏心距離eは基準面上の距離に補正されているものとする。また、角度1ラジアンは、2″×105とする。
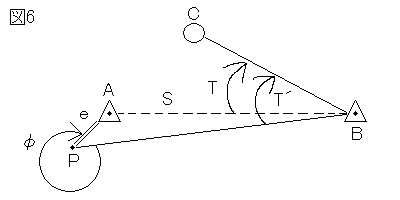
| 既知点A | φ=330°00′00″ |
| e=4.80m | |
| 既知点B | T´=45°37′00″ |
解答手順1(正弦定理)
求めたいのはTの角度です。TはT´-Xで求められます。Xは赤線のところです。まずは表6の数字と、問題文中に登場したSの距離を図に書き込みましょう。青線のところの角度は30°であることが分かるのでそれも書き込んでしまいましょう。ついでに書いておきますが、φはファイと読みます。
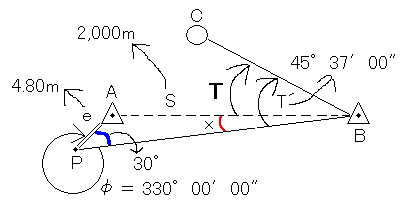
次は公式に数字を当てはめます。偏心補正計算で使う公式は、正弦定理か余弦定理かのどちらかです。大体正弦定理の方を使います。角度を求めたいときに使うのが正弦定理で、辺の長さを知りたいときに使うのが余弦定理です。今回はTを求めるためにT´-Xがしたいので、まだ何度なのかが分かっていないXの角度を求めます。
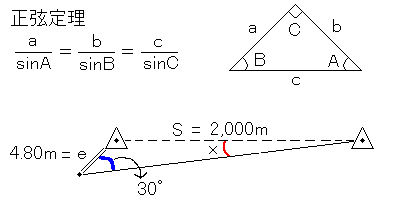
正弦定理より、4.8/sinX = 2000/sin30°
(この問題を解くときには必要のないことですが、分子の単位が揃っていない場合には、計算前に分子の単位を揃えましょう。)
4.8 = 2000/sin30°×sinX
4.8×sin30°/2000 = sinX
(sin30°は0.5です。関数表を参照のこと。)
sinX=4.8×0.5/2000
sinX=2.4/2000
解答手順2(ラジアン)
ここで冒頭のT=T´-Xに数字を当てはめると、T=45°37′00″-2.4/2000になるわけですが、単位が違うので計算ができません。そこで単位を揃えます。単位を揃えるにはラジアンというものを使います。問題文によると角度1ラジアンは、2″×105です。これを2.4/2000に掛けます。
2.4/2000×2″×105
=2.4/2000×2″×100000
(105は100000という意味です。0が5個)
=4.8″/2000×100000
=4.8″/2×100
=2.4″×100
=240″
=4′
(60″(60秒)=1′(1分)なので)
これでT=T´-Xの計算ができます。
T=45°37′00″-4′
=45°33′00″
この問題の答えは45°33′00″です。
ところで土地家屋調査士試験の合格者の約5割を輩出している資格予備校やフルカラーテキストの調査士講座のことをご存じでしょうか? 当サイトおすすめの土地家屋調査士試験、測量士補試験の予備校講座はこちらです。リンク先で詳細をご確認下さい。
通信講座・通学講座・書籍・メディア教材で
資格取得をお手伝いします。
有力資格試験の合格指導専門校 東京法経学院
難関資格試験の通信講座ならアガルートアカデミー
フルカラーテキストの調査士講座
フルカラーテキストの測量士補講座