【土地家屋調査士試験】
平成3年（1991年）度

• 「方向角×斜辺」で求めます。
• 見取図の下にある注意事項2.より、D点からC点に対する方向角は分かっています（170°40′10″です）。
• 斜辺（辺DD´）は三角関数の公式を使って求めます。
• 見取図によると角EDD´は105°4′20″のため、下の画像中のオレンジ色のところの角度は105°4′20″－直角90°＝15°4′20″になります。

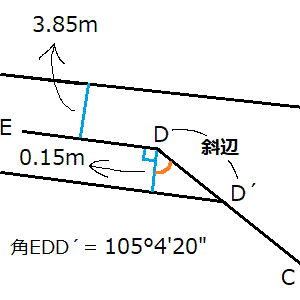
三角関数の公式

• cos15°4′20″×斜辺＝0.15m
  斜辺＝0.1552……（←これが斜辺DD´）

方向角×斜辺

• X座標は、cos170°40′10″×斜辺0.155m＝－0.152985
• Y座標は、sin170°40′10″×斜辺0.155m＝0.02511
  （問題文の下にある注意事項4.により、斜辺は小数点以下第4位を四捨五入しています）

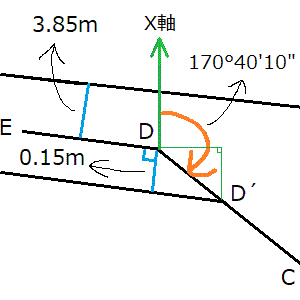
これを点Dに足したのが点D´です（どうして足し算するか）。

D´と同じ方法で求められます。

D´もE´も求め方は「方向角×斜辺」だけでなく、三平方の定理により辺DCや辺EFの長さを求めれば「内分点の公式 or 比の計算」でも座標値は出ます。

見取図の下にある注意事項3.により、点Gは点D´と点E´の中点（真ん中にある点）のため、D´のE´のそれぞれの座標値を足して2で割ったものが点Gになります。