関数表に載っていない数字のルートの取り方

関数表に載っているのは√1～√100までの値なので、たとえば√126のルートを取りたいと思っても、このままでは関数表からその値を知ることができません。そういうときはルートの中身を分解することになります。普通の割り算の筆算の形を、逆にしたような筆算をします。

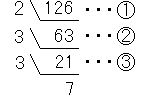
① 126÷2＝63

② 63÷3＝21

③ 21÷3＝7

というわけで、√126は、

√2×√3×√3×√7

＝√2×3×√7

＝3√14

（√14は3.74166です。関数表に載っています。）

＝3×3.74166

＝11.22498

√1.26を例にして解説します。これも√1.26を筆算で分解します。

√1.26

  ＝√126×√0.01

  ＝√126×√0.1×√0.1

  ＝√126×0.1

（√126は11.22498です。1つ上の項目で導きました。）

  ＝11.22498×0.1

  ＝1.122498

√1.26のときは、√1.26を2つに分解した数字のうち、小数点付きのほうが√0.01だったのですぐに0.1に直せました。もしこれが√0.01ではなくて√0.1だったらどうなるか。

ちなみに平成26年（2014年）度の本試験では「2.5√0.5」のルートを取る問題が出ました（No.12）。このルートが取れなくても他の選択肢との比較で答えは出る問題でしたが、ルートが取れるに越したことは無いです。

√12.6

  ＝√126 × √0.1

  ＝√126 × √（1/10）

  ＝√126 × √1/√10

（√1は1です。√10は3.16228です。どちらも関数表に載っています。）

  ＝√126 × 1/3.16228

（√126は11.22498です。このページ内の一番上の項目で導いています。）

  ＝11.22498 × 1/3.16228

  ＝11.22498/3.16228

  ＝3.54～（以下省略）

ところで土地家屋調査士試験の合格者の約5割を輩出している資格予備校やフルカラーテキストの調査士講座のことをご存じでしょうか？ 当サイトおすすめの土地家屋調査士試験、測量士補試験の予備校講座はこちらです。リンク先で詳細をご確認下さい。