土地の面積を求める問題
試験問題 2014年度 No.27
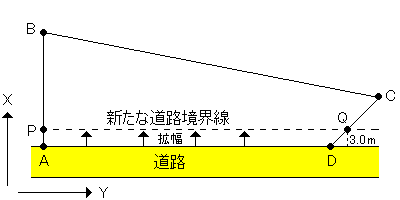
図27は、境界点A、B、C、Dで囲まれた土地を表したものであり、直線ADは道路との境界線となっている。この道路が拡幅（かくふく）されることになり、新たな道路境界線PQが引かれることとなった。直線ADと直線PQが平行であり、拡幅の幅（はば）が3.0 m である場合、点P、B、C、Qで囲まれた土地の面積は幾らか。最も近いものを次の中から選べ。
なお、点A、B、C、Dの平面直角座標系における座標値は、表27のとおりとする。関数の数値が必要な場合は、巻末の関数表を使用すること。
| 点名 | X座標（m） | Y座標（m） |
|---|---|---|
| A | －15.000 | －33.000 |
| B | ＋17.000 | －33.000 |
| C | 0.000 | ＋30.000 |
| D | －15.000 | ＋15.000 |
図27
- 1,115.50㎡
- 1,219.50㎡
- 1,368.00㎡
- 1,462.00㎡
- 1,507.50㎡
解き方
- 図に線を引く。四角形や三角形を作る。問題によっては台形を作ることもある。ちなみに台形の面積を求める公式は、（上底＋下底）×高さ÷2です。
- 表27の数字を使って各辺の長さを算出し、それを図27に書き込む。
- 面積を求める。
図に線を引いて数字を入れる
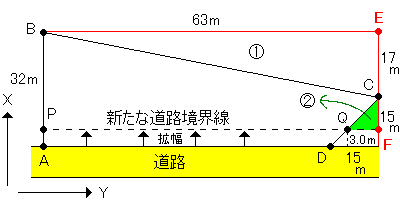
面積を求める
四角形BEFPから三角形①と三角形②を引くと答えが出る。
四角形BEFPは、（32m－3m）×63m＝1827㎡
三角形①は、63m×17m÷2＝535.5㎡
三角形②は、（15m－3m）×（15m－3m）÷2＝72㎡
1827㎡－535.5㎡－72㎡＝1219.5㎡
というわけで答えは2です。
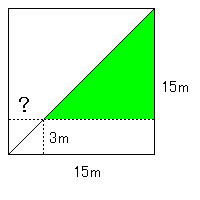
もしかすると三角形②の辺QFの長さが分からない人がいるかもしれませんが、そういう人は15×15の正方形のことを考えてみてください。
