当サイトはアフィリエイトプログラムを利用して商品の紹介を行っています。
縦断測量観測手簿の空欄を埋める問題
試験問題 2014年度 No.26
表26は、ある公共測量における縦断測量の観測手簿の一部である。観測は、器高式による直接水準測量で行っており、BM1、BM2を既知点として観測値との閉合差を補正して標高及び器械高を決定している。表中のア~ウに当てはまる値はそれぞれ何か。次の中から正しい組合せを選べ。
| 地点 | 距離 (m) | 後視 (m) | 器械高 (m) | 前視 (m) | 補正量 (m) | 決定標高 (m) |
|---|---|---|---|---|---|---|
| BM1 | 25.00 | 1.308 | 81.583 | 80.275 | ||
| No.1 | 0.841 | ア | 1.043 | イ | ウ | |
| No.1 GH | 20.00 | 0.854 | 80.527 | |||
| No.2 | 1.438 | 79.943 | ||||
| No.2 GH | 5.00 | 1.452 | 79.929 | |||
| No.2 + 5m | 1.329 | 81.126 | 1.585 | +1 | 79.797 | |
| No.2 + 5m GH | 15.00 | 1.350 | 79.776 | |||
| No.3 | 1.040 | 80.086 | ||||
| No.3 GH | 20.00 | 1.056 | 80.070 | |||
| No.4 | 1.042 | 81.523 | 0.646 | +1 | 80.481 | |
| No.4 GH | 35.00 | 1.055 | 80.468 | |||
| BM2 | 1.539 | +1 | 79.985 |
(GHは各中心杭の地盤高観測点)
- (ア)81.381 (イ) 0 (ウ)80.540
- (ア)81.381 (イ)+1 (ウ)80.540
- (ア)81.381 (イ)+1 (ウ)80.541
- (ア)81.382 (イ) 0 (ウ)80.541
- (ア)81.382 (イ)+1 (ウ)80.541
解き方
図を書いて数字を入れる。この図は水準測量のところで習う「後視」「前視」のことを理解していないと書けない。後視というのは簡単に言うと、測量の始点(この問題だとBM1)の方を向いて(つまり、後ろを向いて)測量をするという意味です。一方、前視は終点(この問題だとBM2)の方を向いて(つまり前を向いて)測量をします。
まずBM1に置いた標尺Aを後視した。
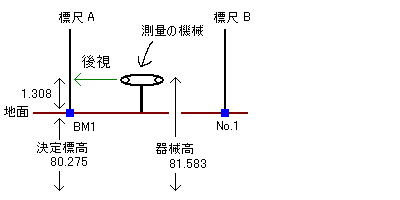
そしてNo.1に置いた標尺Bを前視した。
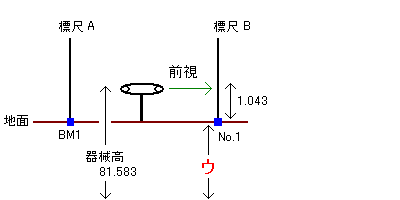
というわけでウは、器械高81.583-前視1.043=80.540です。
次に「測量の機械」と「標尺A」の位置を変えて、No.1の標尺Bを後視した。
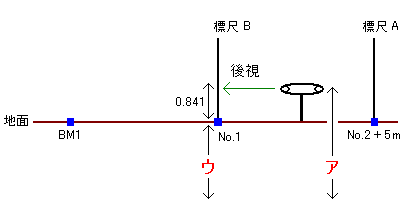
というわけでアは、後視0.841+ウの決定標高80.540=81.381です。
イの求め方(1つ目)
イの求め方は2つあります。
1つ目はそのまま図を書き続けることです。今度は標尺Aを前視します。
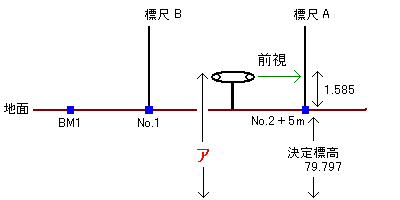
ここで「前視1.585+決定標高79.797=アの器械高81.381」となるはずですが、「前視1.585+決定標高79.797」は81.382なので0.001の誤差が出ていることが分かります。単位はメートルですから0.001m=1mmというわけで+1mmの補正が行われているということです。
では、アやウを求める際にこういう計算違いがあったかというと、そんなものは無かったのでイは0となります。
イの求め方(2つ目)
2つ目は計算です。
BM1は決定標高80.275m、BM2は決定標高79.985mなので、BM1とBM2の標高の差は0.29mです。BM1-0.29m=BM2の標高となります。ところが個々の前視、後視から標高の差を計算してみると、
1.308-1.043=0.265
0.841-1.585=-0.744
1.329-0.646=0.683
1.042-1.539=-0.497
0.265-0.744+0.683-0.497=-0.293
となり、両者には0.003m(=0.3cm=3mm)の差があることが分かります。これがBM1からBM2までの距離全体の補正量です。ここで表26を見てみるとNo.2+5m、No.4、BM2のところでそれぞれ1mmずつ合計3mmの補正があるのでこれ以上は補正されていないことが分かり、イは0となります。
ところで土地家屋調査士試験の合格者の約5割を輩出している資格予備校やフルカラーテキストの調査士講座のことをご存じでしょうか? 当サイトおすすめの土地家屋調査士試験、測量士補試験の予備校講座はこちらです。リンク先で詳細をご確認下さい。
通信講座・通学講座・書籍・メディア教材で
資格取得をお手伝いします。
有力資格試験の合格指導専門校 東京法経学院
難関資格試験の通信講座ならアガルートアカデミー
フルカラーテキストの調査士講座
フルカラーテキストの測量士補講座