当サイトはアフィリエイトプログラムを利用して商品の紹介を行っています。
地図内の建物の経緯度を求める問題
試験問題 2014年度 No.21
図21は、国土地理院発行の電子地形図25000(縮尺を変更、一部改変)の一部である。この図内に示す消防署の経緯度は幾らか。最も近いものを次の中から選べ。
ただし、表21に示す数値は、図内に示す三角点の経緯度及び標高を表す。
図21

| 種別 | 経度 | 緯度 | 標高(m) |
|---|---|---|---|
| 三等三角点 | 東経140°06′00″ | 北緯36°05′36″ | 25.98 |
| 四等三角点 | 東経140°07′02″ | 北緯36°05′23″ | 18.48 |
- 東経140°06′03″北緯36°05′30″
- 東経140°06′07″北緯36°05′26″
- 東経140°06′24″北緯36°05′32″
- 東経140°06′28″北緯36°05′35″
- 東経140°06′55″北緯36°05′34″
求め方その1
地図の経緯度計算は解き方が2種類あると思います。共通しているところから話すと、まずは図21から消防署の地図記号を探します(「Y」に似ている記号が消防署)。
次に表21の標高を参考にして図21から三等三角点と四等三角点の位置を探します(たとえば表21によると三等三角点の標高は25.98となっています。図21の中に記載されている三角点の右横に書いてある数字(これが標高)の中で、この25.98に一番近い数字は26.0なので、その26.0のところの三角点が三等三角点になります。四等三角点の求め方もこれと同じです。表21の標高18.48に一番近い数字である18.5のところの三角点が四等三角点です)。
そして次に三等三角点と四等三角点に定規で十字線を引きます(ここまで共通)。
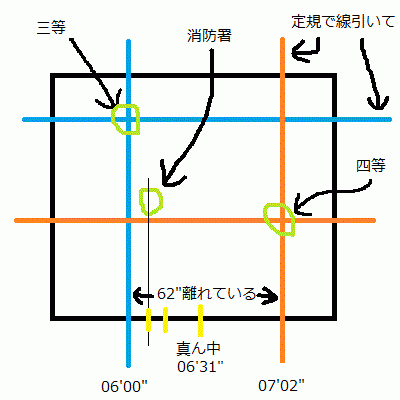
すると特に難しい計算をしなくても、答えは2だと分かってしまいます。三等三角点(東経06′00″北緯05′36″)、四等三角点(東経07′02″北緯05′23″)と答えの選択肢1~5の東経、北緯を比べてみたときに(なおいずれも度数は省略)、
- 東経06′03″北緯05′30″
- 東経06′07″北緯05′26″
- 東経06′24″北緯05′32″
- 東経06′28″北緯05′35″
- 東経06′55″北緯05′34″
たとえば選択肢5の東経06′55″は答えとしてありえないことがすぐに分かると思います。消防署は三等三角点(東経06′00″)の方にすごく近くて四等三角点(東経07′02″)からは離れていますから、位置的に消防署が東経06′55″ということはありえません。
同じように選択肢3と4も切れます。三等三角点の東経06′00″と四等三角点の東経07′02″の真ん中は東経06′31″ですが、そこと比べてもまだ消防署は三等三角点の東経06′00″の方にすごく近いので3と4もありえません。
さらに「三等三角点の東経06′00″」と「先ほど求めた真ん中の東経06′31″」のさらに真ん中を求めてみると東経06′15.5″となり、また同じように「三等三角点の東経06′00″」と「先ほど求めた東経06′15.5″」の真ん中を求めてみると東経06′7.75″となり、東経の位置としては消防署は大体その辺にありますので答えは2となります。
求め方その2
2つ目の解き方は消防署の東経や北緯を厳密に求める方法です。解き方としてはこちらの方がオーソドックスだと思います。定規で距離を測る方法です。

私の手元には平成26年(2014年)度の問題用紙がないので適当な説明になってしまいますが、三等三角点の東経06′00″から四等三角点の東経07′02″までの距離(62″)を定規で測ったときに、仮にそれが10cmだったとして、次に三等三角点の東経06′00″から消防署までの距離を定規で測ったときに、もしそれが1cmだったとしたら(この10cmとか1cmとかいうのは私が勝手に目視で適当に例として出している数字です。本当の正確な距離は手元の問題用紙の図21に定規を当てて測ってみないと分かりません。今、私の手元には問題用紙がありません。他のサイトに掲載されている試験問題を参考にさせてもらっています)、
10センチで62″
では1センチは何秒?
ということで、比の計算をすることになります。
10:62=1:x
10x=62
x=6.2
ということで東経06′00″に6.2″を足すと06′06.2″となり、それに一番近いのは選択肢2の東経06′07″となるため、答えは2となります。なお同じ方法で北緯も求められます。北緯で選択肢を絞り込んでいっても答えは出ます。
ところで土地家屋調査士試験の合格者の約5割を輩出している資格予備校やフルカラーテキストの調査士講座のことをご存じでしょうか? 当サイトおすすめの土地家屋調査士試験、測量士補試験の予備校講座はこちらです。リンク先で詳細をご確認下さい。
通信講座・通学講座・書籍・メディア教材で
資格取得をお手伝いします。
有力資格試験の合格指導専門校 東京法経学院
難関資格試験の通信講座ならアガルートアカデミー
フルカラーテキストの調査士講座
フルカラーテキストの測量士補講座